An age old question from an inquisitive young person: why? Why is the sky blue? Why does one plus one equal two? We will focus on the second specific question today; you are on your own for the sky question. So, why does one plus one equal to two? The answer: it doesn't (always).
The reason we believe that this 1 + 1 = 2 is an immutable fact of the universe is fixed in the fact that we only tend to teach and use one very simple system of mathematics in high school and early college. In particular, all the math we do - all the addition, subtraction, multiplication, division, and so on - is done in a one dimensional (or maybe two-dimensional in early Physics courses) Euclidean space.1 The way that addition is defined for a Euclidean space enforces that 1 + 1 = 2, but it *is* a space-dependent definition. Some spaces - think collections of numbers with rules defining how they relate to each other - do not even have a number two! For example: the space of single-digit binary numbers: 0 and 1. In this number system, 0 + 0 = 0, 1 + 1 = 0, 1 + 0 = 1, and 0 + 1 = 1. There are no other additions to define, which feels bizarre, but is true.
# What is addition, really?
Addition, and its inverse operation subtraction, define a method for moving on a space's associated number system. For the one-dimensional Euclidean space that we are used to from K-12 and early college courses (the real number line), we have a simple number system: a single line which "starts," at zero and extends in one direction (typically left) to negative infinity and the opposite direction (typically right) to positive infinity (pictured below).
Addition is the operation which allows us to step from one point on this line in a positive (typically rightward) direction for the number of units we are adding to our original location. So, if we are starting at the origin, applying the (+ 1) operation to 0 yields: 0 + 1 = 1, because the number 1 is one unit to the right of zero. Likewise, 0 + 2 = 2, because 2 is two units to the right of 0. All sums can be viewed this way in one dimensional Euclidean space. Life gets (slightly) more complicated in higher dimensions, but that's a topic for another day in the not-so-distant future.
# Okay, now what is this 1 + 1 = 0 business?
From basic terminology surrounding computers, most folks have an intuitive notion that there exists some binary number thing that computers use to think. Well, that is essentially correct, if we allow the anthropomorphism regarding the idea that computers can think, vice simply execute prewritten code (despite how magical modern AI large language models may seem).2 But this intuition is not necessarily strong enough with everyone to determine why 1 + 1 = 0 in the smallest version of this space.
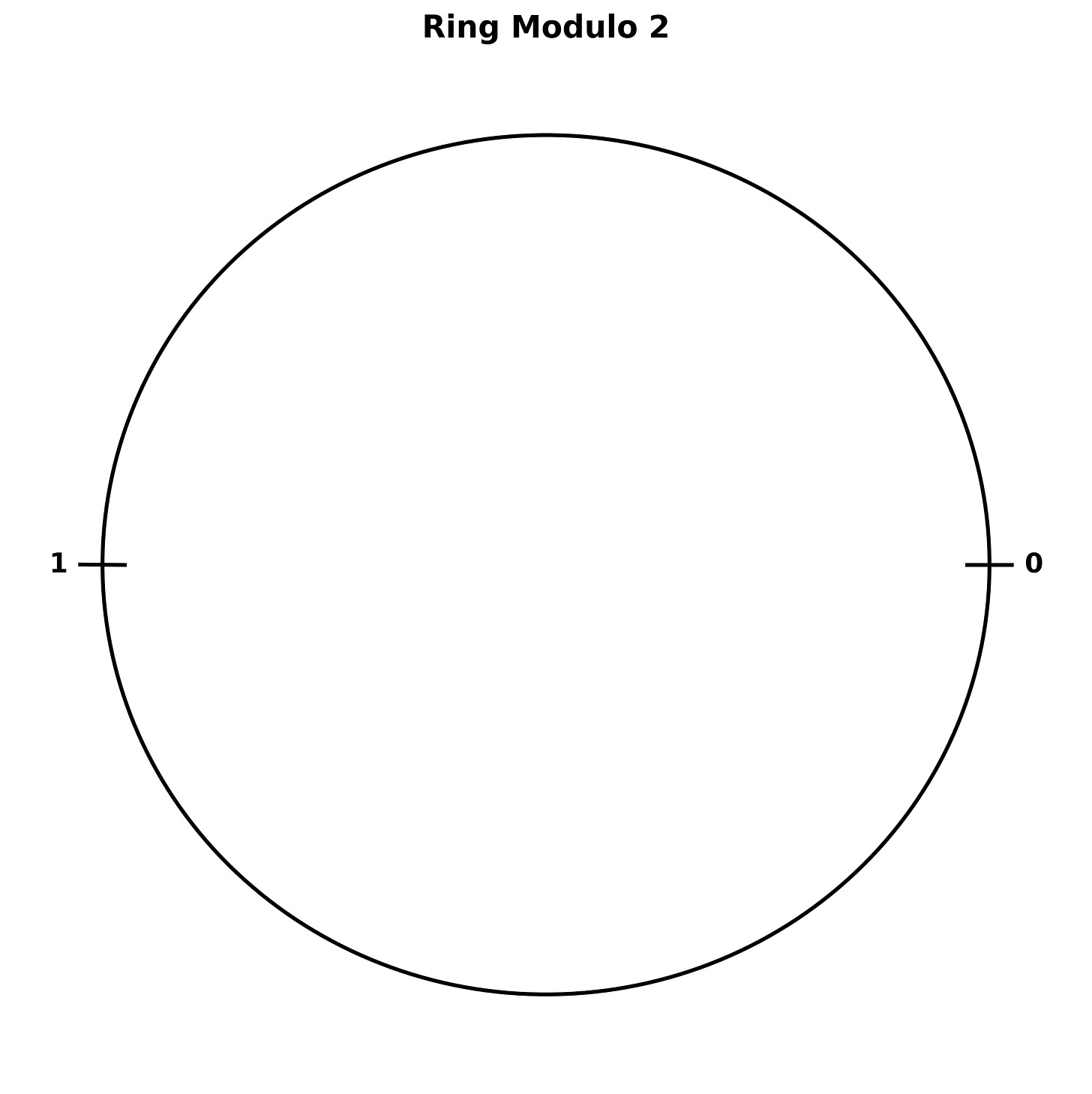
Allow me to elaborate. Not all number systems are simple and linear. A one digit binary system is one such example: it cannot extend forever like the Euclidean system of our shared "simple math," experience, because it only has two values, zero and one. Now, what does "movement," look like in a system with only two values. Everything moves in circles.3 The depiction of the single-digit binary space given below should indicate why.
Moving "right," from 1 by one unit takes you back to 0, because there is no place else to go, look at the figure. Note also, since there is no 2, there is no operation in which 1 + 2 = 1, for those who are curious. You can’t apply operations, even operations which exist in the space, with numbers that do not. Again: the only possible sums which can be evaluated on this space are 0 + 0 = 0, 0 + 1 = 1, 1 + 1 = 0, and the symmetric reflections of each (which includes additionally the sum 1 + 0 = 1).
Now, this explanation falls short of how binary numbers are used for computers to think; rather it only puts for the notion of the problematic “rollover,” that happens with bounded binary number systems that computer engineers must confront in their system designs. I’ll leave binary encodings for a future post, but the essence of the idea is that you can get to much larger numbers before rollover happens by “stacking,” many of the circle-spaces on top of each other, perhaps 64 of them or so are enough for most practical applications.
# Yes, there are (more) practical examples
Can you think of another practical example, now that I've asserted it is possible? Think circles and cycles. I'll give you a minute. Okay, time's up. One is a watch! Or, to be more precise, an analog clockface. In that space, 12 + 1 = 1, and 11 + 2 = 1, and 10 + 3 = 1. Of course 1 + 1 = 2, so that fact remains true in clock-math, but the "familiar," addition does not always work.4
What another example? It's not too far conceptually from the first. You can definitely drive there...its an odometer! When 99999 tips over to 00000, that is another example of adding 1 not resulting in the "next" number. Each individual digit also acts as its own, mini-example as well, if you think closely enough.5
Another example? The dials on spin locks.
Another example? The heat control on a stovetop.
Essentially, whenever we are using math to model *rotational* or *cyclic* motion, addition will be defined differently, such that 1 + 1 may not equal 2. Be wary of circles, cycles, and the like: math can be quite complicated in these settings...which is why they are largely avoided in K-12 settings.
However, I hope I have given you the simple answer to the first grade question: why does one plus one equal two?6 Because math requires moving in number spaces, addition is the simplest, slowest way of moving, and two is one number to the right of one. Want to move faster? Multiply (numbers greater than one). Remember from Session Zero: multiplication is just addition composed with itself a fixed number of times.7
# Conclusion
For the time being, I plan on keeping the next few posts separated from some grand multi-part unifying example. Thus, each of the posts will discuss some fundamental concept or operation which will be useful when we get to our next, grand unifying example - which will be something to do with optimization.
For now, if you’ve find yourself enjoying what you’ve read, consider sharing, subscribing, discussing, and so on. Buttons below for each.
-NJW
A Euclidean space is, loosely, the “most obvious,” generalization of the number line you’d have learned about in elementary school. A picture exist in the body of the post.
For those who aren't forgiving my use of an SAT word, anthropomorphism is the act of assigning the quality of a person to a non-person object. Here, a computer is being assigned the property of being a thinking being, where I am claiming it is not.
That is an Incubus reference, yeah.
The kind of math were are using in all of these examples are called modulo arithmetic, for what it is worth.
In which 9 + 1 = 0.
Note for the curious: I am using the symbolic numbers to refer to when an actual numeric operation is being performed, and the English spelling whenever a conceptual number is being used.
Composition is not something we've explicitly discussed, so allow me a quick definition here. Composing two operations mathematically is to perform them in sequence. So, (5 + 2) - 1 = 6, can be thought of as the addition of 5 and 2 composed with the subtraction of 1. Multiplication is self-composition of addition in that 5 x 3 = 15 is the addition of five composed with itself three times, starting from zero: 0 + 5 + 5 + 5 = 5 x 3 = 15. In the same way, exponents are self-compositional multiplication, but starting from 1 in stead of zero. Can you see why that is true? Why start from one in stead of zero in that case? (Remember: anything times zero is zero.)



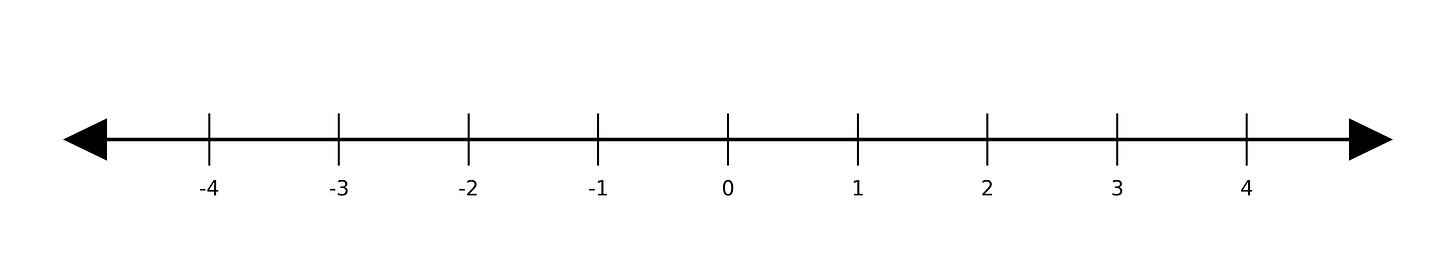
The one example you did give isn't all that convincing to me. One might just as well say that 1 + 1 = 2 = 0 and that two is simply another label for zero in the mod 2 space... I'd be interested to see if there is some area of mathematics, where there is a good reason to define two in a way, such that 1 + 1 = 2 does not hold